[ANN] BackPropagation

• BackPropagation

在[ANN] Perceptron這一篇我們可以得知沒有隱藏層的Perceptron是無法解決XOR的問題，就算我們自行加了隱藏層也沒有對應的演算法去計算隱藏層的值，Paul Werbos於1974提出了BackPropagation Neural Network並解決隱藏層演算的問題。

各參數意義如下：

• X1,X2 ：輸入層，兩個inputs
• H1,H2 ：隱藏層，兩個hidden nodes
• Y：輸出層，一個output
• thetaxh1,thetaxh2 ：隱藏層的bias
• thetahy：輸出層的bias
  

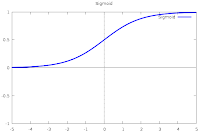
而使用BackPropagation的網路時通常會搭配著以下兩種Transfer Function:

• Sigmoid:

• Hyperbolic Tangent:
  


網路計算公式如下：

如過算出的Y值沒又達到目標值，我們必須計算delta以及更新Weight跟Bias

delta的計算公式如下:



計算weight值

計算Bias值

更新所有的weight和bias

重複上述的運算直到收斂到目標值為止，依據上述的公式我分別使用了C,Java,Perl來實做BackPropagation

Download: BackPropagation.c BackPropagation.java BackPropagation.pl

除了可以比較運行的速度之外，也可以探討精準度，速度方面當然是c語言佔上風，但是精準度卻沒有Java跟Perl，詳細的資料你可以參考下面的網頁。

http://www.adahome.com/History/Steelman/steeltab.htm

在學習速率方面筆者我並沒有讓他們給固定，我使用了下面這行程是碼：

這裡我只是簡單的利用到二次曲線去變動學習速率，而變動依據則是按照目標差距值而定。只是這樣的修改方式並沒有什麼根據，比較好的動態學習速率應該依照DBD,EXDBD或者weight值得觀察來變動，這部份詳細訊息我們之後再來探討。




關於誤差計算方式我則是使用RMSE



當然你可以使用其他方式去計算誤差，RMSE在這個範例裡並不是那麼的重要。輸出畫面如下：

以學習速率0.1為基準，在c語言版本下我們花了0.024秒，算了4000多個epoch之後得到我們的RMSE在0.1以內的解。結果可以說是相當不錯。當然還是有幾個問題需要探討。在多次測試下你可能會發現有時後會收斂不完全，這些問題筆者我會在之後逐一去講解。